Log base e derivative 192293-Log base a derivative

Since the natural log function to the base e (log e e) is equal to 1, The derivative of log e is equal to zero, because the derivative of any constant value is equal to zero Sample Problem Question Solve e x = 62 Solution Given e x = 62 Taking the natural log on both sides, it becomesValue of Log e The power to which a number should be raised to get the specified number is called the logarithm of that number For example, logarithm to the base 10 of 1000 is 3 because 10 raised to the power 3 is 1000 Logarithmic function is the inverse Mathematical function of exponential function The logarithmic function log ax = y isThe expression for the derivative is the same as the one for the original function That is The derivative of e x is e x The derivative of e x is e x This is one of the properties that makes the exponential function really important Now you can forget for a while the series expression for the exponential We only needed it here to prove the

Finding The Derivative Of Log X Video Lesson Transcript Study Com

Log base a derivative

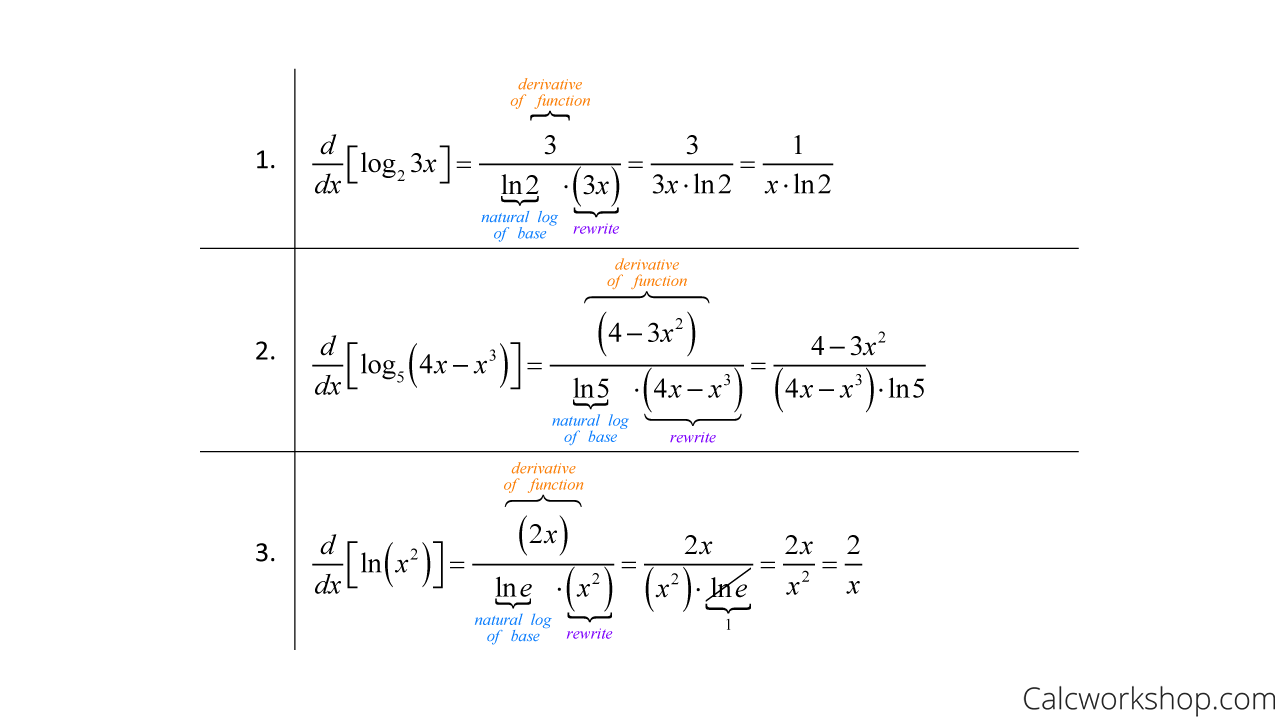
Log base a derivative-The derivative of logₐ x (log x with base a) is 1/(x ln a) Here, the interesting thing is that we have "ln" in the derivative of "log x" Note that "ln" is called the natural logarithm (or) it is a logarithm with base "e" ie, ln = logₑFurther, the derivative of log x is 1/(x ln 10) because the default base of log is 10 if there is no base writtenAnd you notice that the base is omitted in the RHS, it means that it is applicable to any base in the RHS (of course, as long as the same base is used in both numerator and denominator) To me, that is the only acceptable case when one can omit the base

Calculus Exponential Derivatives Examples Solutions Videos

Learn how to solve differential calculus problems step by step online Find the derivative of log(10,x) We can find the derivative of a logarithm of any base using the change of base formula Before deriving, we must pass the logarithm to base e \log_b(a)=\frac{\log_x(a)}{\log_x(b)} Calculating the natural logarithm of 10 The derivative of a function multiplied by a constantA slightly harder example here Let's find the derivative of 100 minus 3 log x Remember, when you see log, and the base isn't written, it's assumed to be the common log, so base 10 log This is the derivative of 100 minus 3 log x I can use the sum rule and constant multiple rule I'll use both at the same time This is the derivative of 100Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers

Finding the derivative of a logarithm with a base other than e is not difficult, simply change the logarithm base using identities If given a function \log_a(b), change the base to e by writing it as \frac{\ln(b)}{\ln(a)}Answer (1 of 7) Assuming That the base to loge is 'e' so that makes it 1 Loge = 1 And that derivative of any constant ie 1 is zero So your answer will be zeroDerivatives of Logarithms and Exponentials The derivatives of the natural logarithm and natural exponential function are quite simple The derivative of ln(x) l n ( x) is just 1 x 1 x, and the derivative of ex e x is, remarkably, ex e x d dx (ln(x)) = 1 x d d x ( l

As the logarithmic function with base , and exponential function with the same base form a pair of mutually inverse functions, the derivative of the logarithmic function can also be found using the inverse function theorem Suppose we are given a pair of mutually inverse functions and Then In the particular case , the derivative is given by This is the formula $$\frac{d}{dx}\log_bx=\frac{1}{x\ln b}$$ How can it be proved?Traditionally, to evaluate the derivative of a power function, one would have to either resort to logarithmic differentiation, or basee standardisation before differentiating it With the advent of the Exponent Rule, both of these approaches basically become obsolete — not because they are irrelevant per se, but because they have already

5 Derivative Of The Logarithmic Function

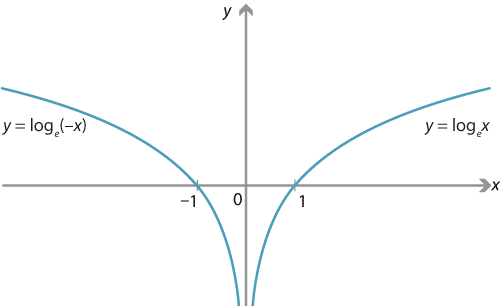
Content The Natural Logarithm

The derivative of the base e exponential function is just that Don't get comfortable, though We'll have to use the Chain Rule to differentiate these, but at least it makes it easier without consulting a list of derivativesFirst Derivative of a Logarithmic Function to any Base The first derivative of f(x) = log b x is given by f '(x) = 1 / (x ln b) Note if f(x) = ln x , then f '(x) = 1 / x Examples Example 1 Find the derivative of f(x) = log 3 x Solution to Example 1 Apply the formula above to obtain f '(x) = 1 / (x ln 3) Example 255 Exponential Bases other than e TOOTLIFTST • Knowledge of derivatives of basic functions, including power, exponential, logarithmic, trigonometric, and inverse trigonometric functions We have already seen how easy it is to work with the exponential and logarithmic bases e, but as you can imagine, not all the problems we will come in

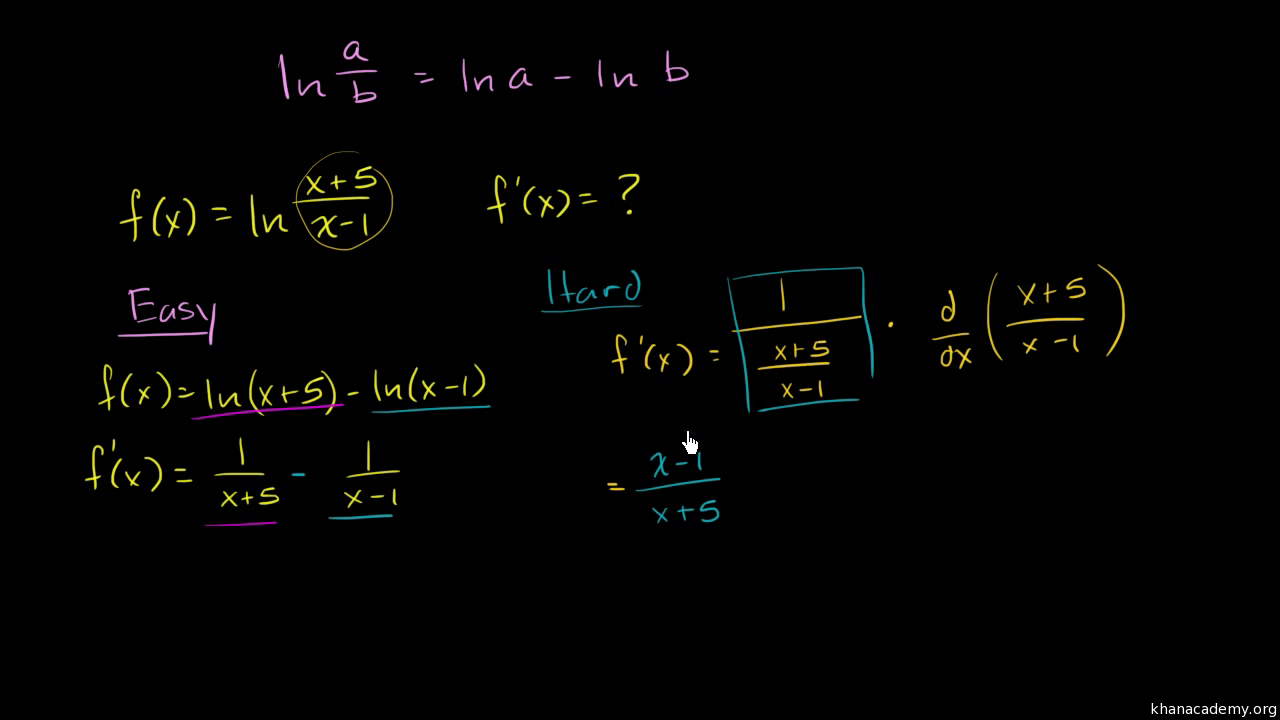
Differentiating Logarithmic Functions Using Log Properties Video Khan Academy

Finding The Derivative Of Log X Video Lesson Transcript Study Com

Derivative of logₐx (for any positive base a≠1) Practice Derivatives of aˣ and logₐx Worked example Derivative of 7^ (x²x) using the chain rule Worked example Derivative of log₄ (x²x) using the chain rule This is the currently selected item Worked example Derivative of sec (3π/2x) using the chain ruleIn mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formula ′ where ′ is the derivative of f Intuitively, this is the infinitesimal relative change in f;We start with the function y = l n ( x) First use exponentiation with the base e to get rid of the log, a common manipulation with log equations, e y = x (*) Now take the derivative of each side, remembering to use the chain rule on ey, because y is a function of x d d x e y = d d x x and

Finding The Derivative Of Log X Video Lesson Transcript Study Com

Finding Derivatives Of Logs And Natural Logs Krista King Math Online Math Tutor

The derivative of y=\ln(x) can be calculated by using implicit differentiation on x=e^y, solving for y, and substituting for y, which gives \frac{dy}{dx}=\frac{1}{x} Calculus Differentiating Logarithmic Functions Differentiating Logarithmic Functions with Base e Key Questions What is the derivative of #f(x)=ln(x)/x# ?Derivatives of sin (x), cos (x), tan (x), eˣ & ln (x) Derivative of logₐx (for any positive base a≠1) Worked example Derivative of log₄ (x²x) using the chain rule Practice Differentiate logarithmic functions Differentiating logarithmic functions using log properties Derivative of Differentiating Logarithmic Functions with Bases other than e If u = f(x) is a function of x, and y = log b u is a logarithm with base b, then we can obtain the derivative of the logarithm function with base b using `(dy)/(dx)=(log_be)(u')/u` where `u'` is the derivative of u log b e is a constant

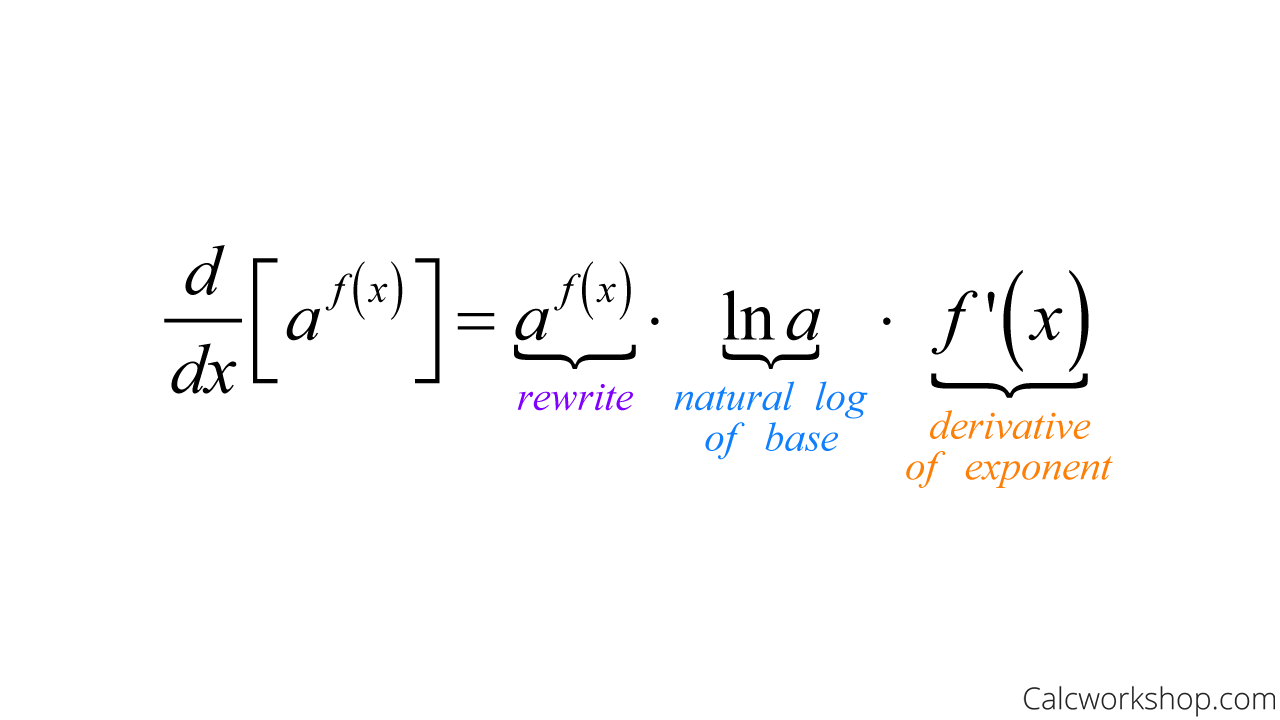
Derivatives Of Logarithmic Functions Fully Explained

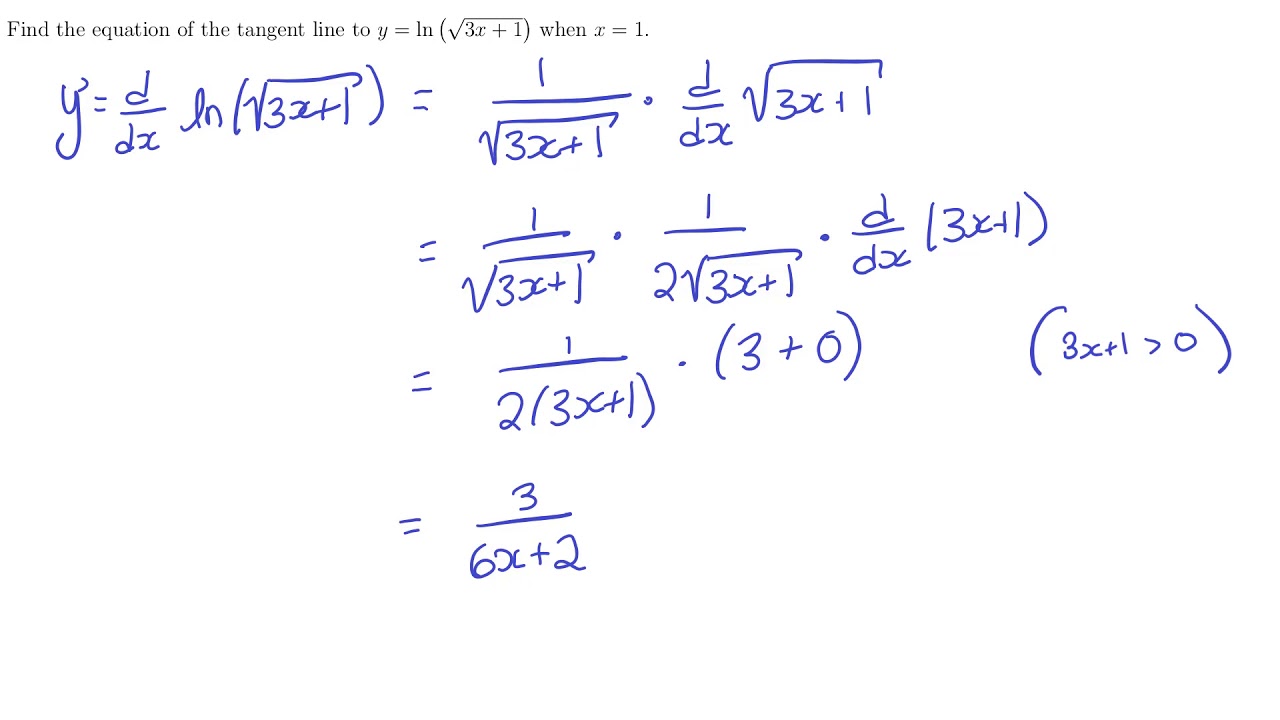
Derivatives Of Exponential Logarithmic Functions

Logz gives the natural logarithm of z (logarithm to base e) Logb, z gives the logarithm to base bProblem 5 The derivative of log a x According to the rule for changing from base e to a different base a Topic of Precalculus Calculate the limit of that derivative a) when x is greater than 1 and becomes larger That derivative approaches 0, that is, becomes smaller b) when x is less than 1 and becomes smaller That derivative becomes That is, ln ( x) = log e ( x ) Okay, so let's use this formula to find the derivative of log ( x ) We have that the base of log ( x) is 10, so we plug this into the derivative formula for log a

Derivative Of Ln X Natural Logarithm More

Objectives For Section 11 2 Derivatives Of Exp Log Functions Ppt Download

Find the Derivative d/dx f (x) = log base 9 of x f (x) = log9 (x) f ( x) = log 9 ( x) The derivative of log9(x) log 9 ( x) with respect to x x is 1 xln(9) 1 x ln ( 9)Derivatives of logarithmic functions are mainly based on the chain ruleHowever, we can generalize it for any differentiable function with a logarithmic function The differentiation of log is only under the base e, e, e, but we can differentiate under other bases, tooIt follows, then, that if the natural log of the base is equal to one, the derivative of the function will be equal to the original function This is exactly what happens with power functions of e the natural log of e is 1, and consequently, the derivative of ex e x is ex e x d dx ex = ex d d x e x = e x

Derivative Of Exponential Function Fully Explained

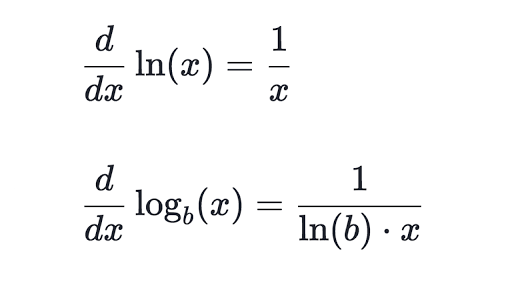
Differentiating Logarithmic Functions Review Article Khan Academy

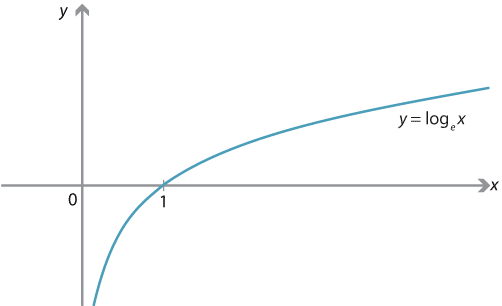
The notation lnx is short for log e x and the function lnx is called the natural logarithm The derivative of y = lnx can be obtained from derivative of the inverse function x = eyOur online Derivative Calculator gives you instant math solutions with easy to understand stepbystep explanations e = Euler's number, the base of the exponential function ( Please rewrite the logarithm using logarithmic identitiesFree derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graph

5 Derivative Of The Logarithmic Function

3

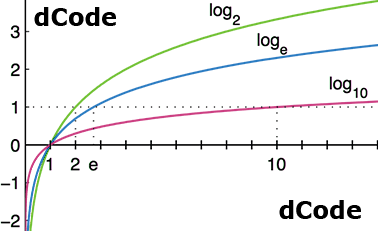
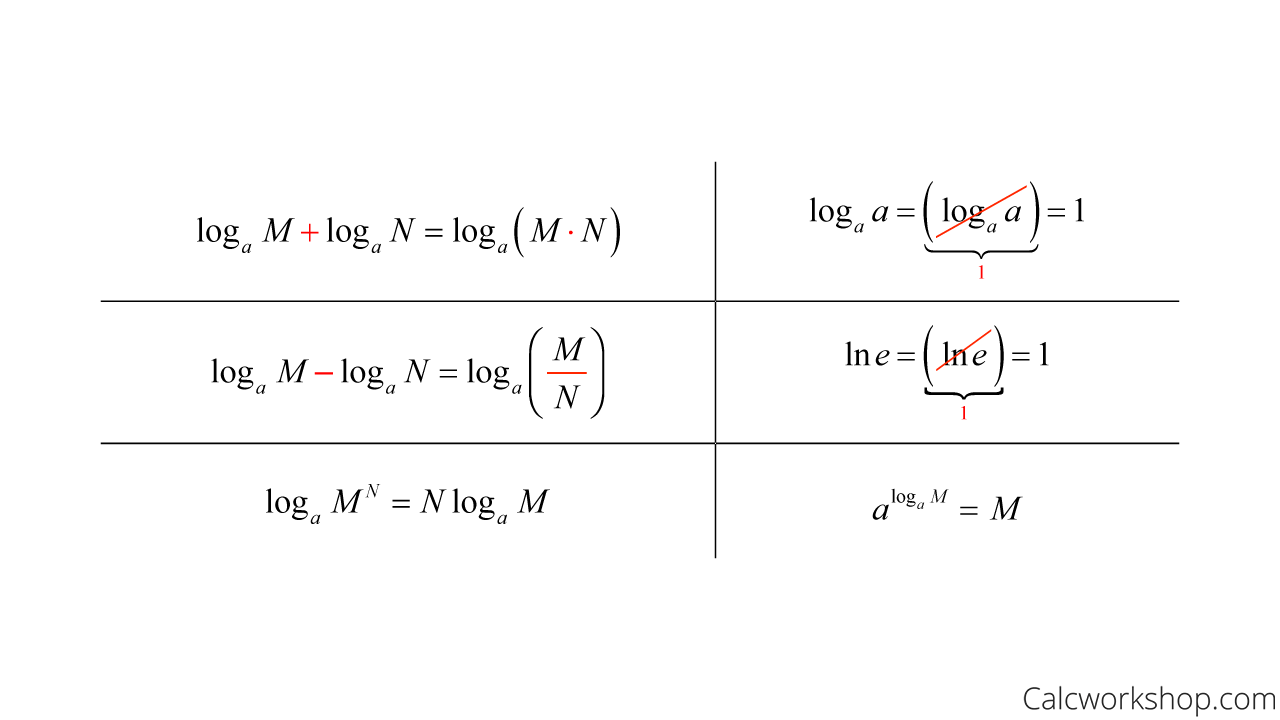
That is, the infinitesimal absolute change in f, namely ′, scaled by the current value of f citation neededWhen f is a function f(x) of a real variable x, andY = f ( x) = log a x First we take the increment or small change in the function y Δ y = log a ( x Δ x) Δ y = log a ( x Δ x) – y Putting the value of function y = log a x in the above equation, we get Δ y = log a ( x Δ x) – log a x Δ y = log a ( x Δ x x) Δ y = log a (Logarithm base change rule The base b logarithm of x is base c logarithm of x divided by the base c logarithm of b log b ( x) = log c ( x) / log c ( b) For example, in order to calculate log 2 (8) in calculator, we need to change the base to 10 log 2 (8) = log 10 (8) /

5 Derivative Of The Logarithmic Function

Logarithm Wikipedia

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2718 281 8 459The natural logarithm of x is generally written as ln x, log e x, or sometimes, if the base e is implicit, simply log x Parentheses are sometimes added for clarity, giving ln(x), log e (x), or log(x)Another video addresses functions with base ehttp//mathispower4uwordpresscom/The derivative of e with a variable exponent is equal to e with that exponent times the derivative of that exponent • We care because nature does not usually go by logs, but instead by natural logs We write "log base e" as

Natural Logarithm Wikipedia

Derivative Of Logarithm For Any Base Old Video Khan Academy

36 Derivatives of Logarithmic Functions Math 1271, TA Amy DeCelles 1 Overview Derivatives of logs The derivative of the natural log is (lnx)0 = 1 x and the derivative of the log base bis (log b x) 0 = 1 lnb 1 x Log Laws Though you probably learned these in high school, you may have forgotten them because you didn't use them very muchThe natural log function of 10 is denoted as "log e 10" It is also known as the log function of 10 to the base e The natural log of 10 is also represented as ln(10) The value of log e 10 is equal to log e 10 = ln (10) = Log Values from 1 to 10 Some of the values of log functions to the base 10 from the value of log 1We defined log functions as inverses of exponentials \begin{eqnarray*} y = \ln(x) &\Longleftrightarrow & x = e^y \cr y = \log_a(x) & \Longleftrightarrow & x = a^y \end{eqnarray*} Since we know how to differentiate exponentials, we can use implicit differentiation to find the derivatives of $\ln(x)$ and $\log_a(x)$

7 4 Logarithmic Differentiation

Derivative Of Logₐx For Any Positive Base A 1 Video Khan Academy

Find the Derivative d/dx y = log base 4 of x y = log4 (x) y = log 4 ( x) The derivative of log4(x) log 4 ( x) with respect to x x is 1 xln(4) 1 x ln ( 4) 1 xln(4) 1 x ln ( 4)Derivative of Logarithm When the logarithmic function is given by f ( x) = log b ( x) The derivative of the logarithmic function is given by f ' ( x) = 1 / ( x ln ( b) ) x is the function argument b is the logarithm base ln b is the natural logarithm of b For example when The number e frequently occurs in mathematics (especially calculus) and is an irrational constant (like π)Its value is e = 2718 281 8 Apart from logarithms to base 10 which we saw in the last section, we can also have logarithms to base eThese are called natural logarithms We usually write natural logarithms using `ln`, as follows `ln x` to mean `log_e x`

Finding Derivatives Of Logs And Natural Logs Krista King Math Online Math Tutor

Natural Logarithm Wikipedia

Logarithmic function and their derivatives Recall that the function log a x is the inverse function of ax thus log a x = y ,ay = x If a = e;Logarithmic differentiation Calculator online with solution and steps Detailed step by step solutions to your Logarithmic differentiation problems online with our math solver and calculator Solved exercises of Logarithmic differentiation

The Derivative

Warm Up Six Chapter 5 5 Derivatives Of Base Not E 11 Ppt Download

5 Derivative Of The Logarithmic Function

Derivatives Of Logarithmic Functions Fully Explained

5 Derivative Of The Logarithmic Function

Solved Find The Derivative Of A Logarithmic Function That Is Chegg Com

Logarithm Calculator Natural Log Base 2 E 10 N Online Log2 Log10

How Do You Find The Derivative Of E X Log X Socratic

If Math Y E Log Sin X Math Then What S The Derivative Quora

Content The Natural Logarithm

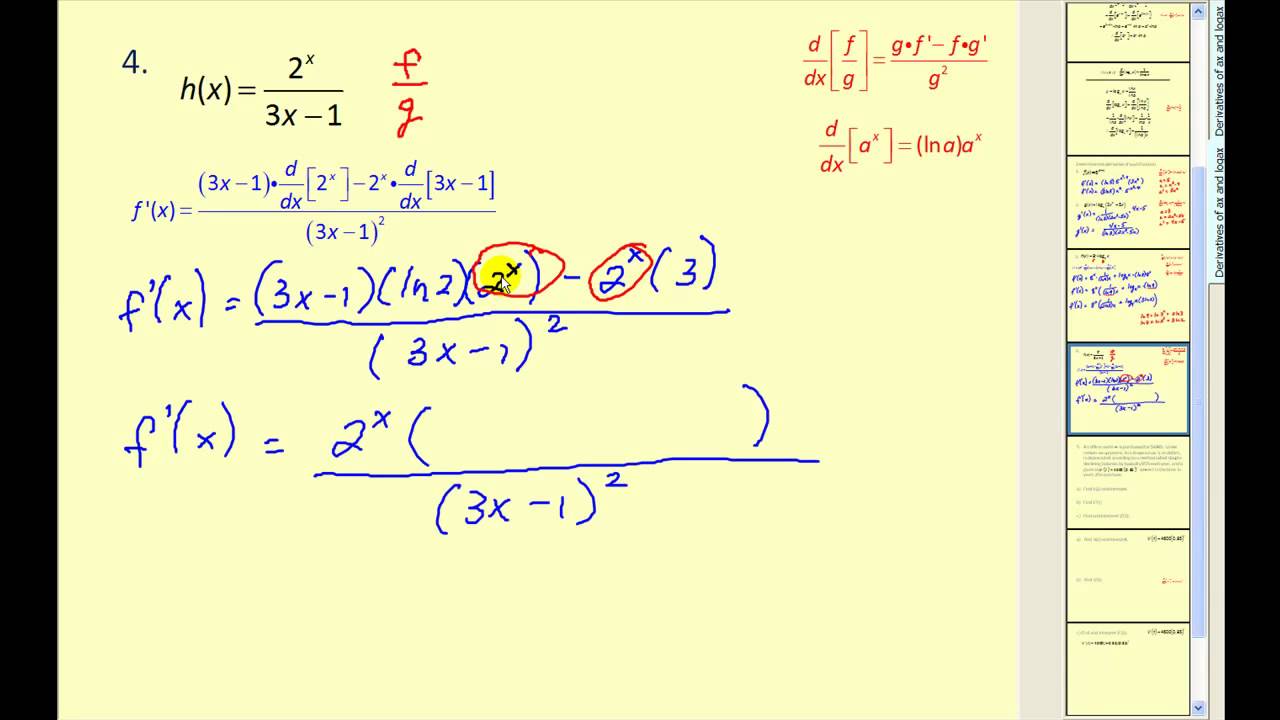
The Derivatives Of Exponential And Logarithmic Functions Base Not Equal To E Youtube

Derivatives Of Logarithmic Functions Fully Explained

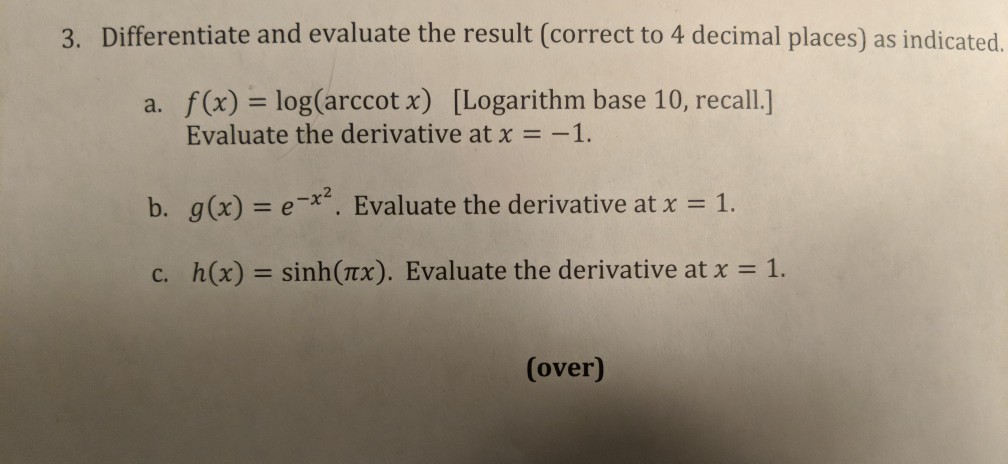
Solved 3 Differentiate And Evaluate The Result Correct To Chegg Com

Derivatives Of Exponential Functions Logarithmic Differentiation Calculus Lnx E 2x X X X Sinx Youtube

1

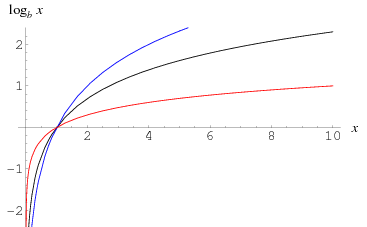
Logarithm From Wolfram Mathworld

Finding The Derivative Of Log X Video Lesson Transcript Study Com

1

1

Derivatives Of Logarithmic Functions Problem 3 Calculus Video By Brightstorm

Derivative Of Log Y Mathematics Stack Exchange

Derivatives Of Exp And Log With Base Not E Youtube

The Derivative

Difference Between Log And Ln Physicscatalyst S Blog

Chapter 5 Section 5 5 Bases Other Than E And Applications Ppt Download

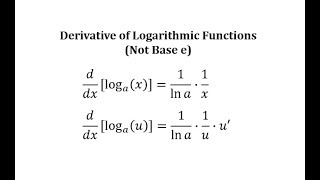
Ex 1 Derivative Of The Log Function Not Base E Youtube

What Is The Derivative Of E Logx Quora

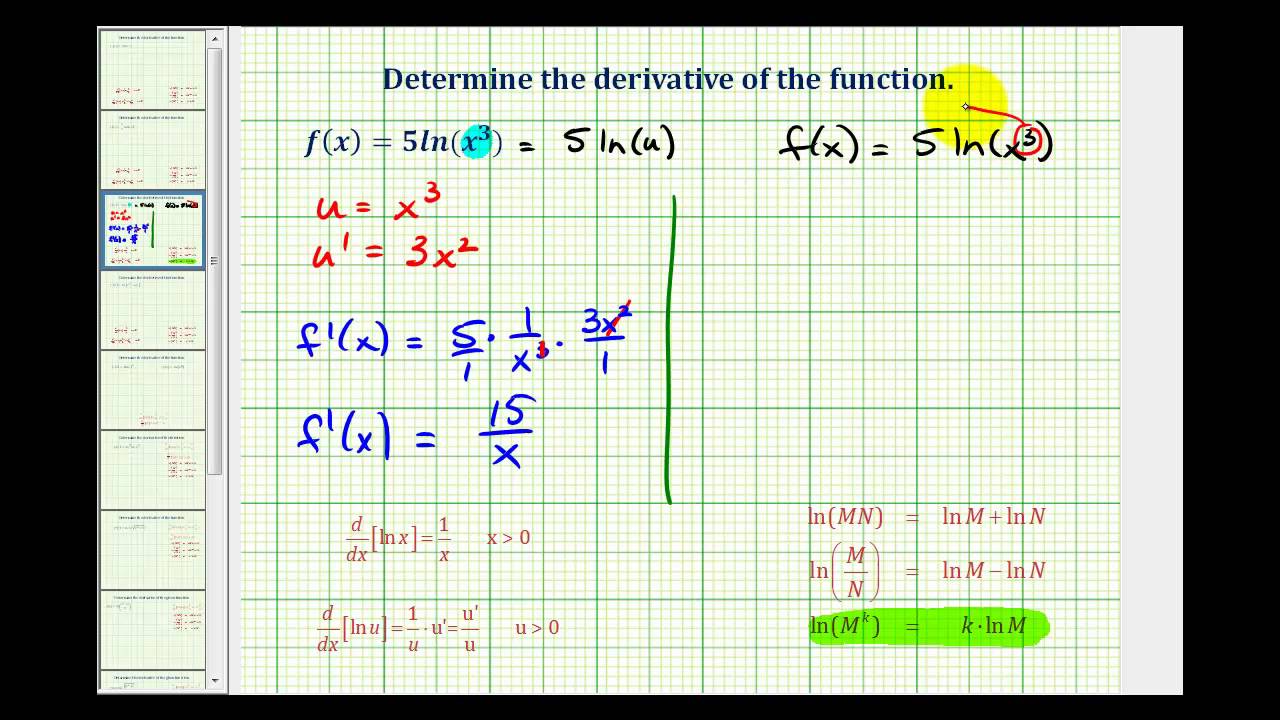
Calculus Derivative Of The Natural Log Ln Video Lessons Examples Solutions

Derivative Of Log Confusion Mathematics Stack Exchange

Ex 1 Derivatives Of The Natural Log Function Basic Youtube

Solved Suppose We Needed To Calculate The Second Derivative Chegg Com

Part 4 4 Logarithmic Function Log Ax Derivative Of Exponential Logarithmic Functions Youtube

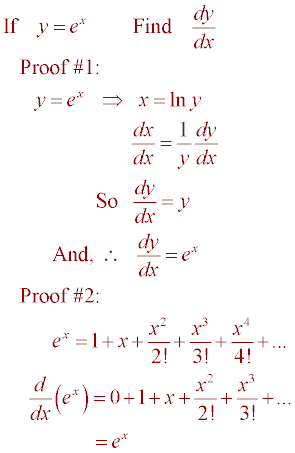
Lesson 52 Derivatives Of Exponential Functions

How To Find The Derivative Of Log Base A Of X Quora

Calculus Exponential Derivatives Examples Solutions Videos

What Is The Differentiation Of Log X To The Base E And Log X To The Base 10 Quora

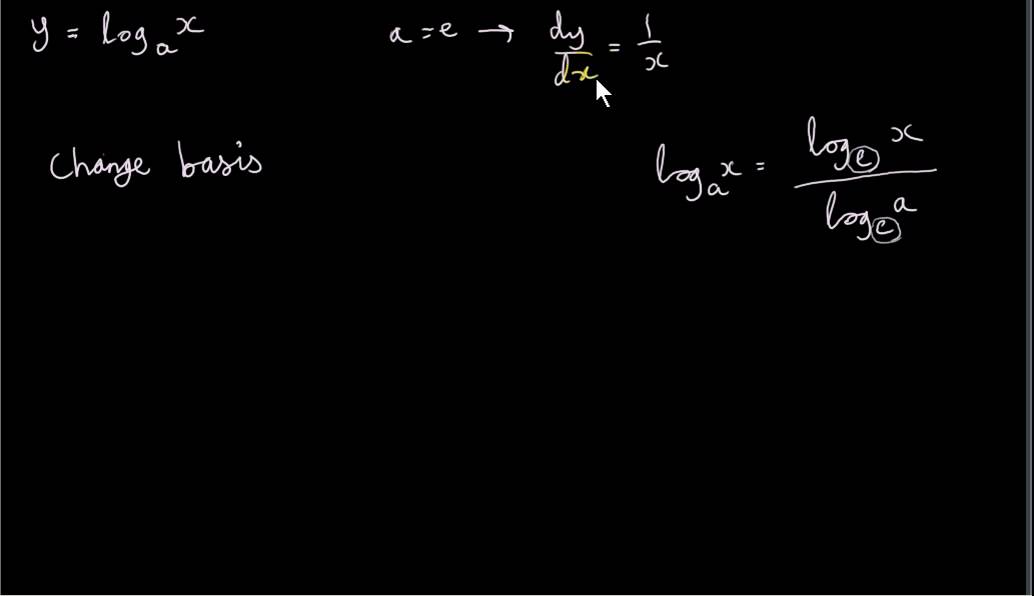
The Derivative Of Y Log X For Any Positive Base A Youtube

D Dx Log Exp Functions

5 Derivative Of The Logarithmic Function

2

Bases Other Than E Ap Calc Notes

Solved Calculate The Derivative Of Y 4 Log X 1 The Log Chegg Com

Solved Derivatives Of Logarithmic Functions Calculate The Derivative Of The Following Functions In Some Cases It Is Useful To Use The Properties Of Logarithms To Simplify The Functions Before Computing F Prime X Y Log

Finding The Derivative Of Log X Video Lesson Transcript Study Com

The Derivative Of A Logarithm If F X Log A X Then Notice If A E Then Ppt Download

5 Derivative Of The Logarithmic Function

Derivative Of A Function Is Called The Derivative

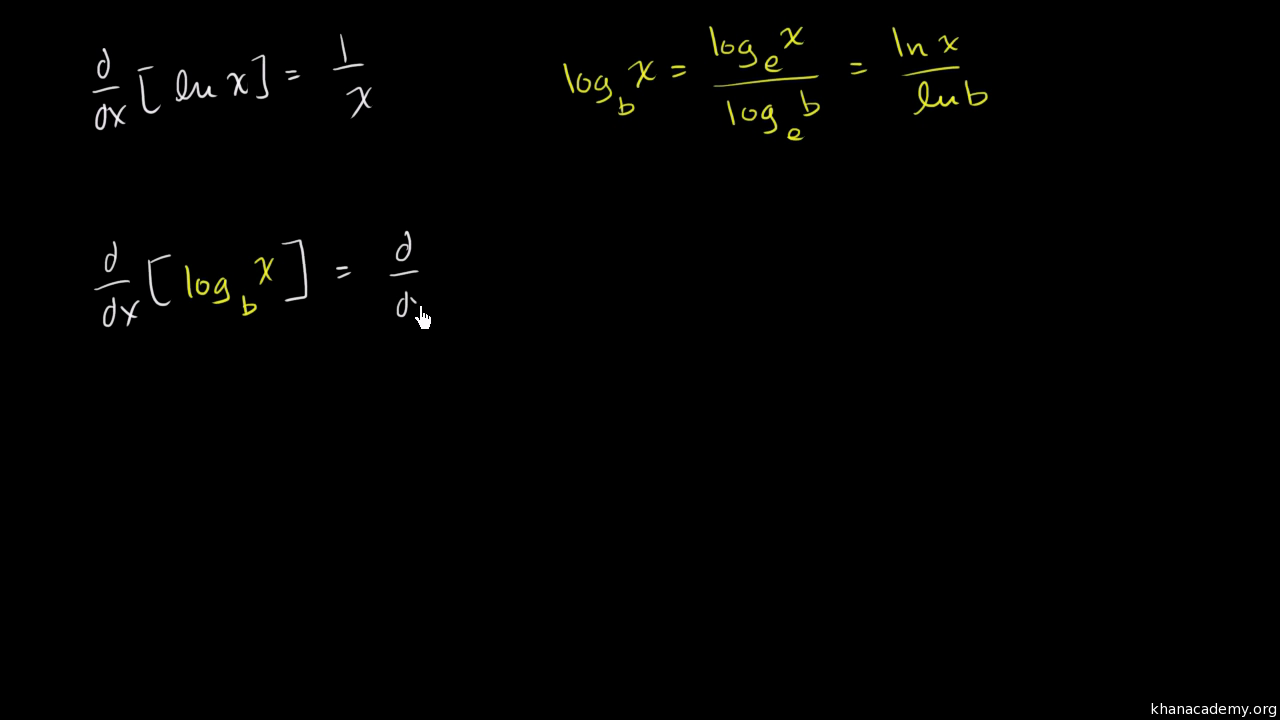
Derivative Of Logarithm For Any Base Old Video Khan Academy

8 2 Derivatives Of Logarithmic Functions

Copyright C Cengage Learning All Rights Reserved 11 Techniques Of Differentiation With Applications Ppt Download

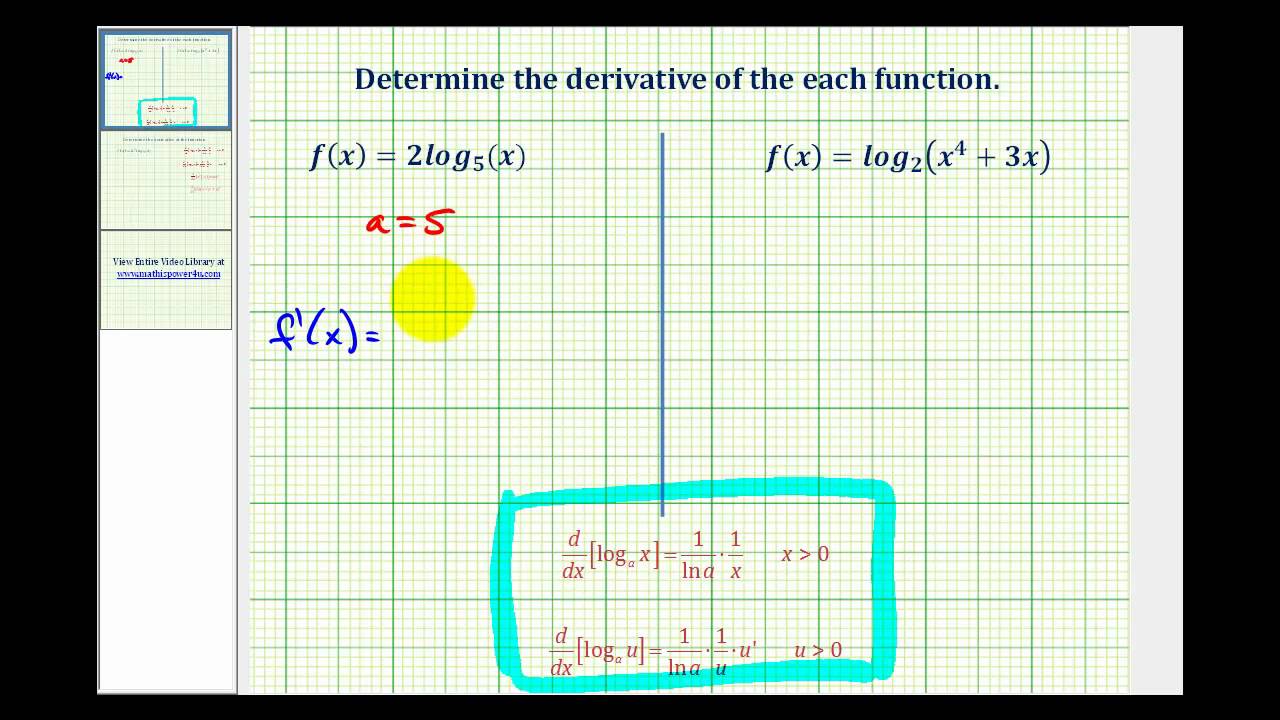
New Version Available Ex 1 Derivative Of The Log Function Not Base E Youtube

Derivatives Of Exponential Logarithmic Functions

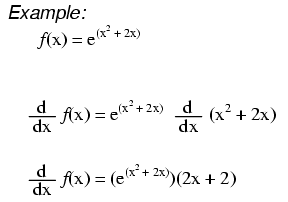
Derivatives Of Power Functions Of E Calculus Reference Electronics Textbook

Derivatives Definition Of A Derivative Differentials Rules For Differentials

Calculus 6 3c Derivatives Of Base B Logarithms Youtube

Logarithmic Differentiation Calculator Peatix

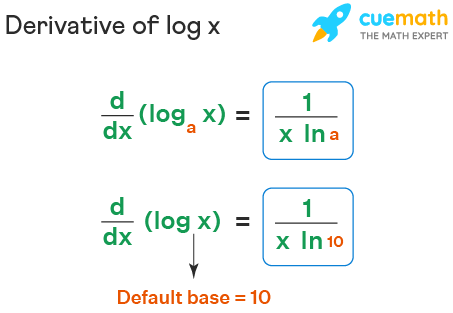
Derivative Of Log X Formula Proof Examples

Derivatives Of Logarithmic Functions Fully Explained

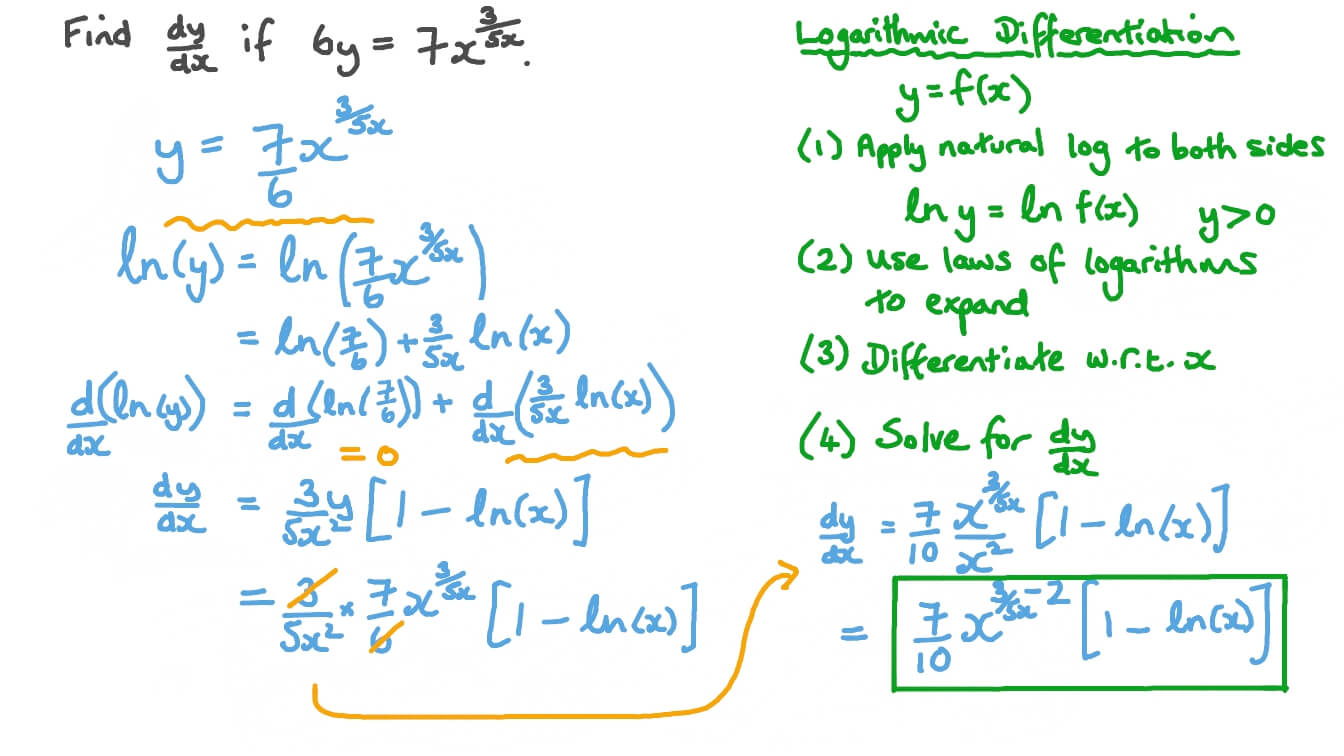
Question Video Finding The First Derivative Of A Function Having A Variable In Its Base And Exponent Using Logarithmic Differentiation Nagwa

Mathcamp321 Calculus Derivatives Of Logs With Bases Not E 5 5 Youtube

2

Exponent Rule For Derivative Theory Applications Math Vault

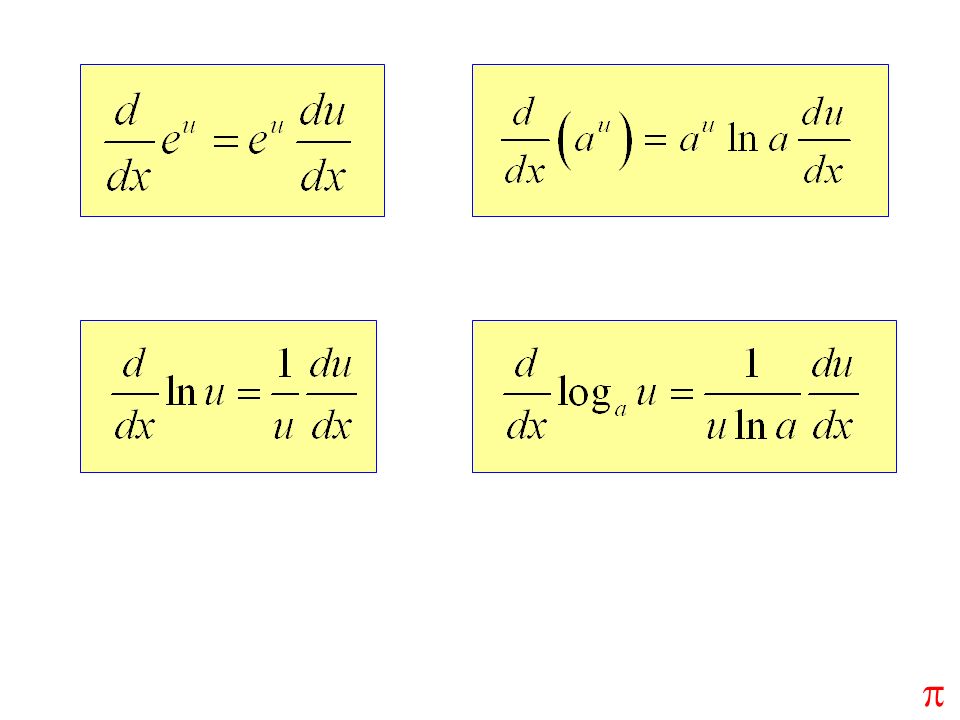
3 9 Derivatives Of Exponential And Logarithmic Functions Ppt Download

Natural Logarithm Wikipedia

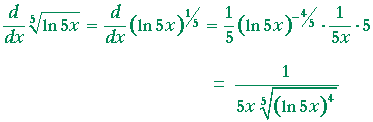
Derivatives Of Exponential And Logarithmic Functions An Approach To Calculus

What Is The Derivative Of Log 2 Quora

Cbse Class 12 Differentiation Of Log Base E X And Log Base A X From First Principles In Hindi Offered By Unacademy

Randolph H S Ap Calculus Ab 09 Derivatives Of Exponential Logarithmic And Inverse Trigonometric Functions

Derivative Of Log Base 10 Of X 3 1 With The Box Youtube

Techniques Of Differentiation Ppt Download

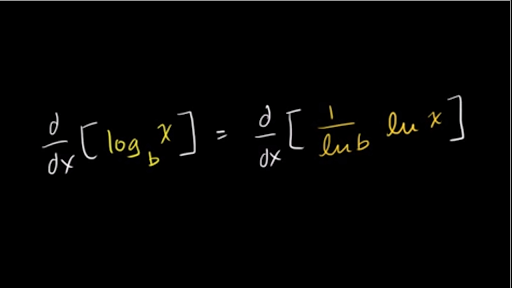
Derivative Of Logarithm For Any Base Old Video Khan Academy

Derivative Of Logarithm For Any Base Old Video Khan Academy

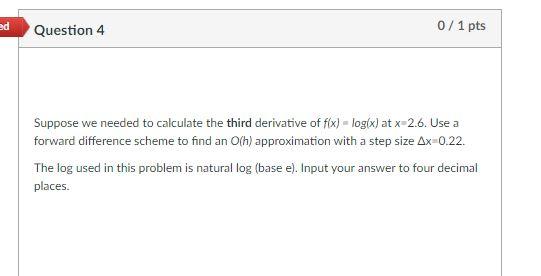
Solved Ed Question 4 0 1 Pts Suppose We Needed To Calculate Chegg Com

What Is The Differentiation Of Log Base X Of A Quora

What Is The Value Log E Quora

3 9 Derivatives Of Ln General Exponential Log Functions And Logarithmic Differentiation Mathematics Libretexts

What Is The Derivative Of X 2 Log X Quora

5 5 Bases Other Than E And Applications Ppt Download

Derivative Of Log Base 10 Detailed Login Instructions Loginnote

Derivative Of Log Confusion Mathematics Stack Exchange

Calculus Derivative Of The Natural Log Ln Video Lessons Examples Solutions

What Is The Differentiation Of Log X To The Base E And Log X To The Base 10 Quora

Incoming Term: log base a derivative, log base derivative, derivative of log base e,